Journey of magic books
MAT 259, 2022
Zijian Wan
Concept
I'm interested in how often books about learning magic are checked out and how
long they have been kept (read). So, I ran the following query to obtain relevant
book checkout records.
Query
SELECT
*
FROM
spl_2016.inraw
WHERE
(title LIKE '%magic%'
AND (title LIKE '%learn%'
OR title LIKE '%beginners%'
OR title LIKE '%tricks%'))
AND YEAR(cout) BETWEEN 2006 AND 2021;
*
FROM
spl_2016.inraw
WHERE
(title LIKE '%magic%'
AND (title LIKE '%learn%'
OR title LIKE '%beginners%'
OR title LIKE '%tricks%'))
AND YEAR(cout) BETWEEN 2006 AND 2021;
Preliminary sketches
The records were obtained as a CSV file and preprocessed with Python (codes
attached below, "dataPreprocessing.pdf").
Each checkout/checkin record is visualized as a trajectory from the date the book was checked out to the date it was checked in. The coordinates of the points that consist of a trajectory are computed as follows. The z coordinate represents the distance from the plane of that circle. Since the distance between two adjacent year circles is fixed (which corresponds to 365 days), the z coordinate can be calculated according to the days that the book has been kept by the reader. The x and y coordinates are computed based on a polar coordinate system as shown in the figure below. Note that both the angle phi and the length l are determined by the month and day. In this way, the visualization form (which is like flowers) is actually determined by the data instead of manually designed.
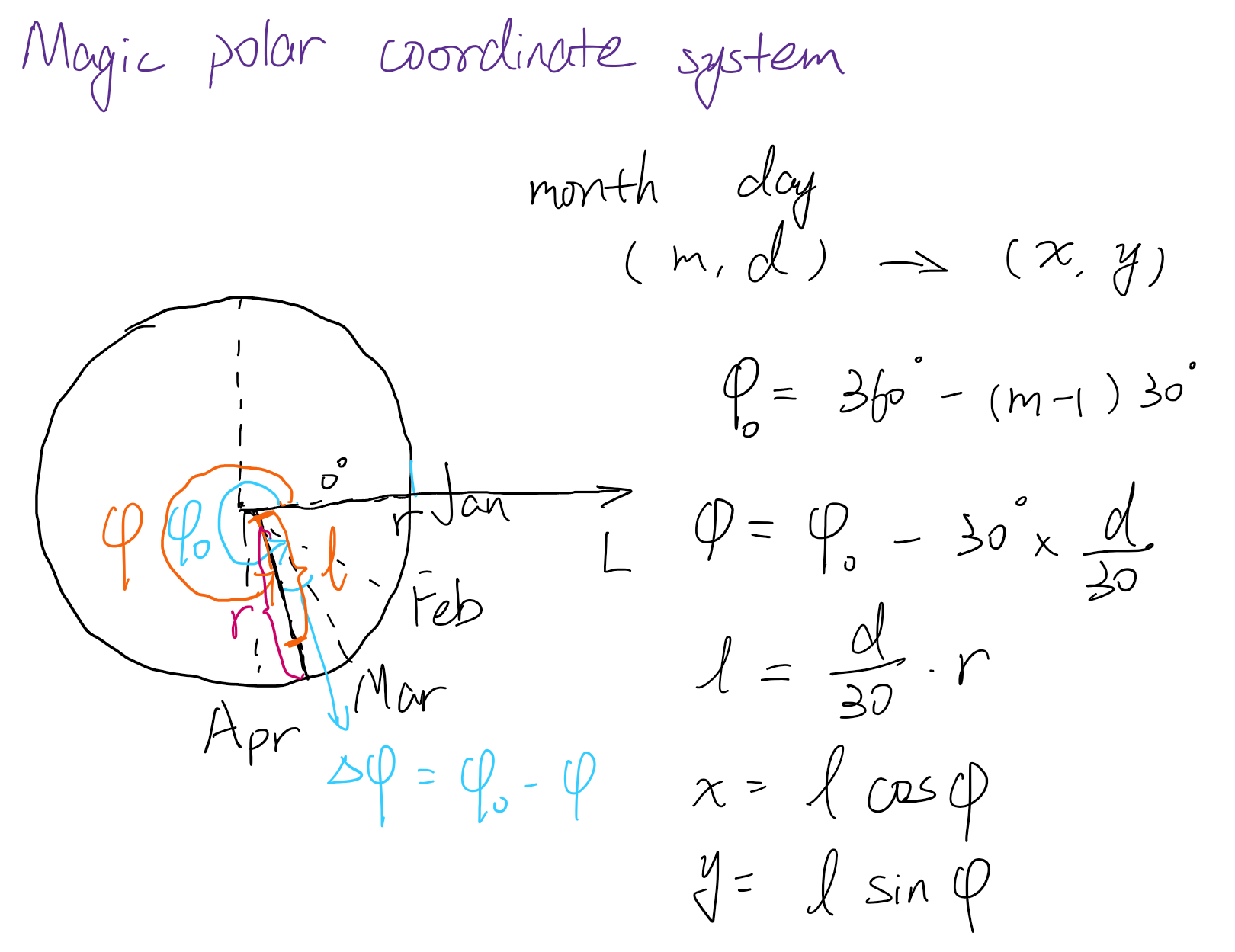
Each checkout/checkin record is visualized as a trajectory from the date the book was checked out to the date it was checked in. The coordinates of the points that consist of a trajectory are computed as follows. The z coordinate represents the distance from the plane of that circle. Since the distance between two adjacent year circles is fixed (which corresponds to 365 days), the z coordinate can be calculated according to the days that the book has been kept by the reader. The x and y coordinates are computed based on a polar coordinate system as shown in the figure below. Note that both the angle phi and the length l are determined by the month and day. In this way, the visualization form (which is like flowers) is actually determined by the data instead of manually designed.

Process
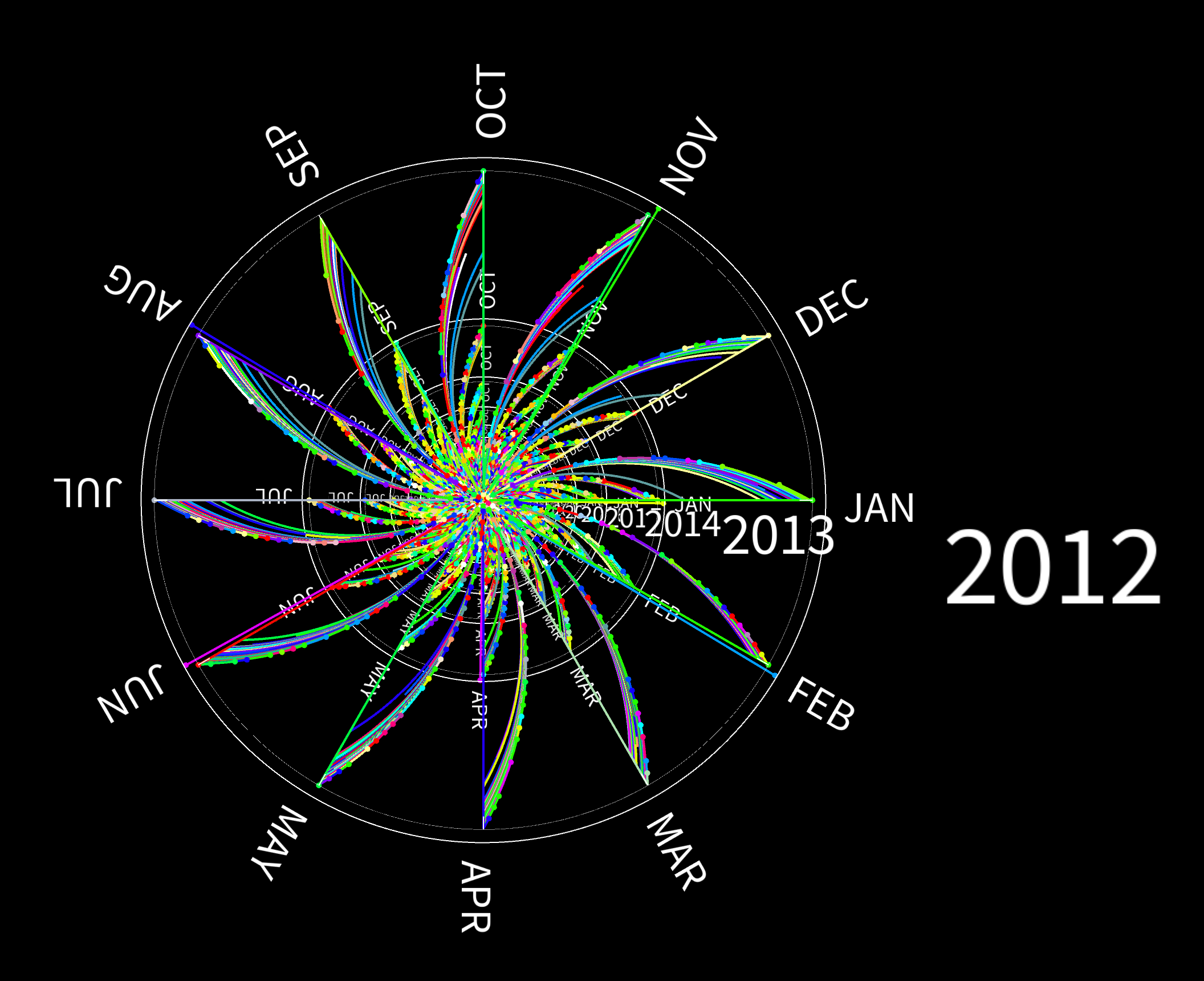
Then, I visualized the records in Processing. For each year, there is a circle.



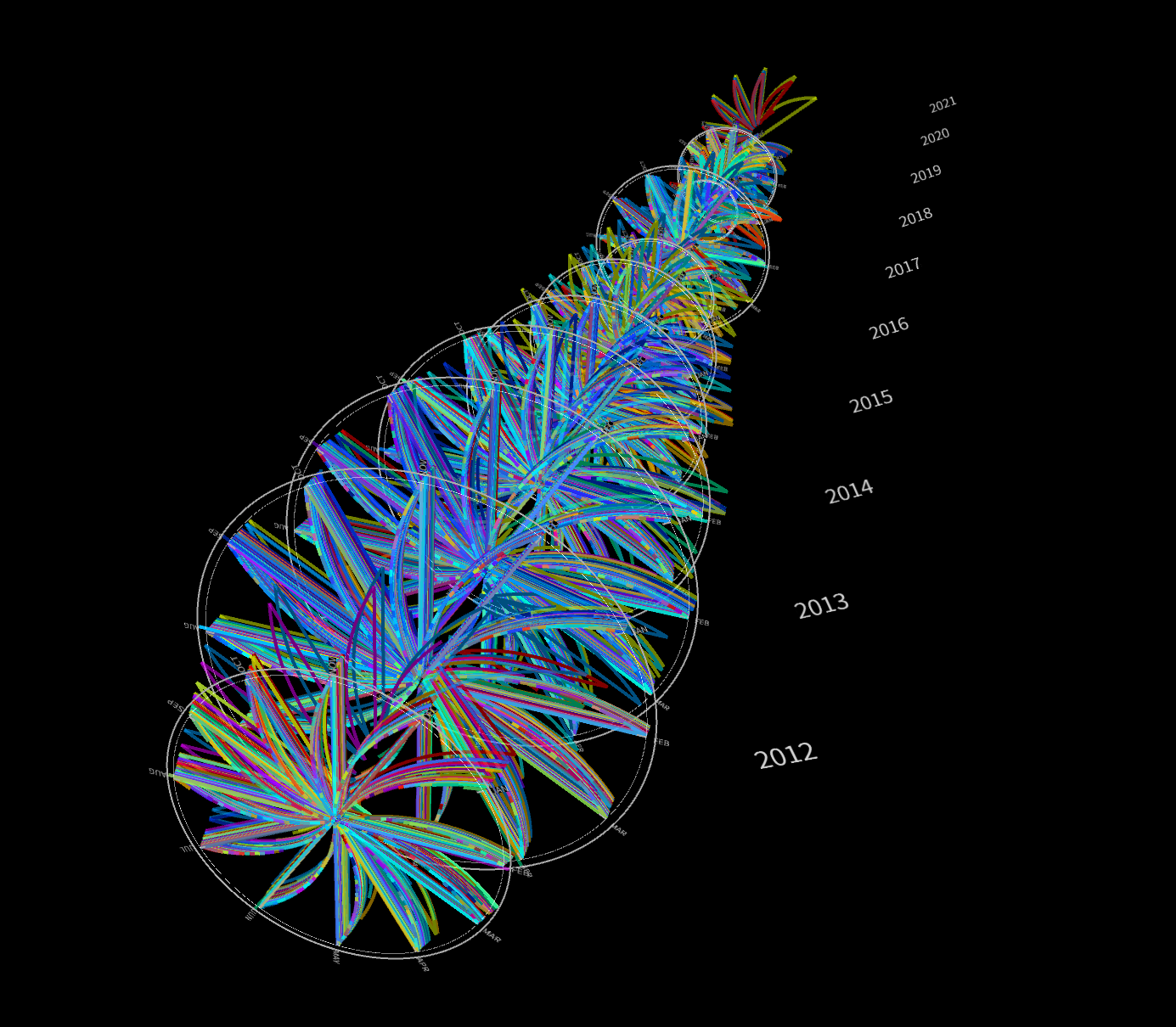
Final result
I changed the radius of each circle to represent the total number of checkouts of
that year and the colors were updated for asethetic reasons.



Code